PCTO Matematica e Comunicazione nel Bridge – Catania, DMI, 2022
Copyleft
![]() 2022 Giuseppe Scollo
2022 Giuseppe Scollo
Non sempre la deduzione nel Bridge dà risposte certe alle domande che si presentano nel gioco... esempi:
Il calcolo delle probabilità dà risposte incerte, con un margine di incertezza matematicamente definito. Questa lezione ha un duplice obiettivo:
Si deve sempre tener conto dell'informazione da altre fonti: queste possono determinare la certezza di eventi che condiziona la probabilità della risposta
Richiami di concetti e definizioni utili alla deduzione probabilistica nel Bridge
Una premessa concettuale, per sgombrare il campo da possibili equivoci:
La differenza fra i due concetti trova esempi nella fase di licita del Bridge:
Le 39 distribuzioni possibili costituiscono una partizione dell'insieme delle estrazioni (senza ripetizioni) di 13 carte da un insieme di 52 carte distinte
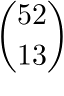
La probabilità di ciascuna distribuzione, delle 13 carte nei 4 colori, è data dal rapporto fra il numero di combinazioni che essa classifica e la cardinalità dello spazio campionario, in particolare:
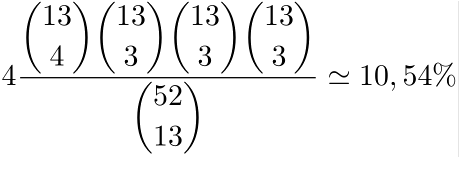
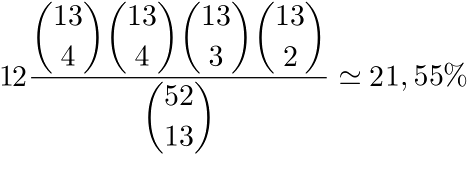
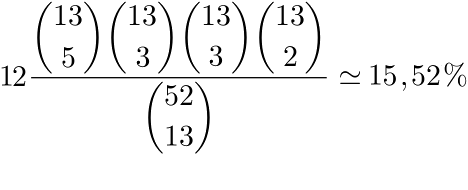
tuttavia, essendo nota la dichiarazione a NT, lo spazio campionario si riduce al sottospazio delle sole distribuzioni bilanciate
i rapporti fra le tre probabilità restano invariati
la somma delle tre probabilità, condizionate da questa informazione, dev'essere 1 (100%)
La divisione dei resti più vantaggiosa non è necessariamente la più probabile
esempio: la divisione 3-3 dei 6 resti è la più vantaggiosa, ma non la più probabile:
p(3-3) = 35,53%, p(4-2) = 48,45%, p(5-1) = 14,53%, p(6-0) = 1,49%
Come si calcolano queste probabilità? Notazione :
Lo spazio campionario (casi possibili) è l'insieme delle estrazioni di 13 carte da 26 (ciascuna estrazione di una mano degli opponenti determina quella dell'altra mano)
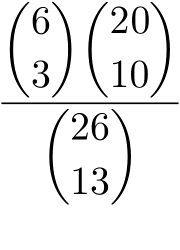 , p(4-2) =
, p(4-2) =
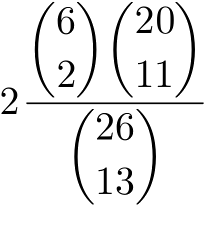 , p(5-1) =
, p(5-1) =
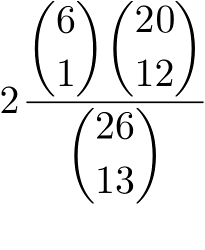 , p(6-0) =
, p(6-0) =
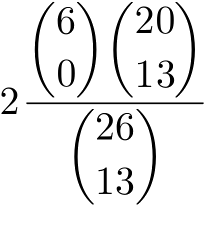
E1.1 Probabilità condizionata
La domanda posta a pag. 5 riguarda un'asserzione che vale più in generale: Sia S/≈ la partizione di uno spazio campionario S da una relazione di equivalenza ≈. Chiaramente, le classi di ≈-equivalenza sono eventi mutuamente incompatibili. Sia E l'evento unione di un insieme di tali classi del quale è nota l'impossibilità. Questa informazione riduce lo spazio campionario al complemento di E in S e fa crescere proporzionalmente le probabilità degli altri eventi, mantenendone i rapporti. Come si spiega questo in base alla definizione di probabilità condizionata? Qual è il fattore di proporzionalità per il quale crescono dette probabilità?
E1.2 Probabilità di divisioni dei resti
È utile sapere che, se in linea mancano r carte in un colore, la divisione dei resti più probabile è:
Nei seguenti esempi: a) calcolare la probabilità della divisione dei resti
nel caso più probabile;
b) determinare in tale caso il numero di prese certe nel colore.
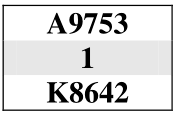
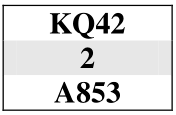
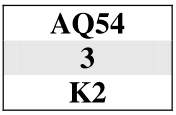
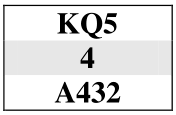
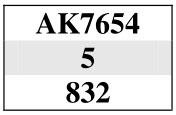
Quando in un colore si hanno in linea la maggioranza delle carte e la testa del colore, ma manca un onore, occorre decidere se battere in testa o tentare l'impasse per la sua cattura
In assenza di altri indizi sulla collocazione dell'onore mancante:
Notazione : p(n|m) = probabilità che l'onore mancante sia n-simo se mancano m carte
Fatti : p(n|2n)=p(n-n) ; p(n|n)=p(n-0) ; n+k=m, n>k>0 ⇒ p(n|m)+p(k|m) = p(n-k)
è dunque molto semplice calcolare le probabilità di divisioni dei resti con un onore mancante dalle probabilità delle divisioni dei resti, v. prossimo esercizio
E2.1 Calcolo semplificato delle probabilità di divisioni dei resti con un onore mancante
Spiegare perché valgono i primi due fatti enunciati sopra, e come il terzo giustifichi il seguente metodo di calcolo: n+k=m, n>k>0 ⇒ p(n|m) = (n/m)p(n-k), p(k|m) = (k/m)p(n-k)
E2.2 Rapporto fra probabilità di divisioni dei resti simmetriche con un onore mancante
Dimostrare che n+k=m, n>k>0 ⇒ p(n|m)/p(k|m)=n/k
Suggerimenti :
Generalizzare, usando le variabili m,n,k nelle ipotesi dell'antecedente
dell'implicazione, il metodo impiegato negli esempi del testo allegato
di A. Squellati, pp. 18-19, a una formula per il calcolo di p(n|m),
quindi applicarla anche al calcolo di p(k|m), e infine semplificare
il rapporto usando l'antecedente dell'implicazione e la nota proprietà
di simmetria dei binomiali:
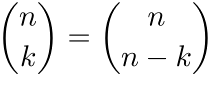
E2.3 Battere in testa o tentare l'impasse?

La cattura della Q è l'obiettivo del Giocante (Sud), che può scegliere fra due tattiche alternative: a) battere in testa, giocando i suoi onori nei primi due giri, oppure b) tentare l'impasse alla Q, sperata in Ovest, e reiterarla se non cade. Probabilità delle divisioni dei 5 resti: p(3-2) = 67,83%, p(4-1) = 28,26%, p(5-0) = 3,91%. Che probabilità di successo hanno le due tattiche?
La comunicazione, sia nella licita che con il gioco delle carte, veicola informazione, che può modificare le probabilità di determinati eventi
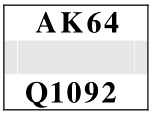
per esempio, nel caso in figura, dalle probabilità della divisione dei 5 resti, v. Esercizio E2.3, possiamo calcolare la probabilità che l'onore mancante
sia non più che terzo come somma delle probabilità degli eventi 1|5, 2|5 e 3|5, e poiché l'unione degli eventi 2|5 e 3|5 è l'evento 3-2:
p(n<4|5) = p(1|5)+p(2|3)+p|3|5) = p(4-1)/5+p(3-2) = 5,65%+67,83% = 73,48%
Come ricalcolare le probabilità degli eventi residui?
Questo può determinare cambiamenti di decisioni tattiche? Per esempio, una decisione iniziale del Giocante di battere in testa? Sì! Infatti...
... nell'esempio in considerazione:
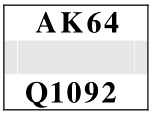
cambiare in corso d'opera una decisione iniziale del Giocante di battere i tre onori?
Supponiamo che il gioco vada così:
La probabilità a posteriori di un evento è valutata dopo l'arrivo di informazione che la modifica rispetto alla probabilità a priori, valutata prima
Riconsideriamo l'esempio mostrato a pag. 6: è un caso particolare dell'ultimo esempio presentato in Sez. 4.2 del testo di A. Squellati

Per catturare il J, Nord batte i due onori e gli opponenti giocano cartine nel colore, quindi gioca il 10 ed Est risponde allo stesso modo: qual è il rapporto fra le probabilità che il J sia a Ovest o a Est?
Correttamente, il testo argomenta che il gioco visto esclude gli eventi 6-0 e 5-1, e dimezza l'evento 4-2 poiché dalla terza cartina da Est si deduce che la divisione dei resti 4-2 è possibile solo se le 4 carte sono a Est. Gli eventi residui 3-3 e 4-2 fissano la posizione del J: a Ovest nella 3-3, a Est nella 4-2. Il calcolo che così ne risulta darebbe la probabilità a posteriori :
Tuttavia, se si ragiona in base alle probabilità a priori delle divisioni dei resti con un onore mancante, usando il metodo semplificato di calcolo esposto nell'Esercizio E2.1, e si effettua il ricalcolo delle probabilità a posteriori p(3|6) e p(4|6), si ottiene un risultato diverso, v. Esercizio 3.1:
Come mai? Sorge il sospetto che in uno dei due metodi di calcolo non si sia tenuto conto di tutta l'informazione che è possibile dedurre dalla dinamica del gioco osservata
Fissiamo inanzitutto un principio:
Per sciogliere l'enigma, facciamo ricorso alla cosiddetta teoria dei posti liberi
Per valutare il rapporto fra le probabilità che l'onore mancante si trovi a Est o a Ovest, dopo il gioco della terza cartina da Est, consideriamo che:
e in effetti 11/10 = 52,38/47,62, come dal secondo metodo nella pagina precedente
E3.1 Probabilità a posteriori
E3.2 Probabilità di successo di una tattica
Nell'esempio discusso a pag. 12, la decisione di battere l'A dopo la terza cartina giocata da Est è una conferma della tattica iniziale di battere in testa i tre onori per catturare l'onore mancante.
Come si calcola il numero (39) delle distribuzioni possibili? Occorre elencarle tutte?
No, lo si può calcolare per ricorrenza
Un paio di definizioni :
Proprietà :
Diagramma di Ferrers (5,3,3,2)

Per il numero delle distribuzioni si calcola P13,4 (usando per brevità Pn,2 = 1+⌊n/2⌋)
P13,4 =
P13,3 +
P9,4
=
P13,2 +
P10,3 +
P9,3 +
P5,4
=
7 + P10,2 +
P7,3 +
P9,2 +
P6,3 +
P5,3 +
P1,4 =
ecc. = 7+6+4+3+1+5+4+2+1+3+2+1 = 39
Se vuoi contar le pecore, conta le zampe e dividi per 4
Senso matematico della regola: richiede alcuni concetti di teoria degli insiemi
Senso matematico della regola del pastore: se S è un insieme finito e ≈ su S induce classi di equivalenza che hanno tutte la stessa cardinalità k, allora |S/≈| = |S|/k
Le combinazioni di k elementi estratti da un insieme di n elementi, con k < n, sono semplici se senza ripetizioni, cioè i k elementi sono tutti distinti (come nelle estrazioni del Lotto)
quante sono? È il numero C(n,k) dei sottoinsiemi di cardinalità k di un insieme di cardinalità n ... per calcolarlo richiamiamo due concetti, dove la qualifica “semplici” ha sempre lo stesso significato: elementi tutti distinti
Per calcolare il numero di combinazioni semplici, definiamo una relazione di equivalenza sulle sequenze per ignorare l'ordine in cui vi compaiono gli elementi:
applichiamo quindi la regola del pastore e introduciamo la notazione dei coefficienti binomiali :
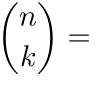 D(n,k)/k! = n(n-1)...(n-k+1)/k! = n!/k!(n-k)!
D(n,k)/k! = n(n-1)...(n-k+1)/k! = n!/k!(n-k)!
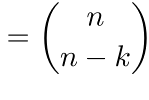
Perché si chiamano coefficienti binomiali?
Diamo per acquisite le definizioni di spazio campionario U e di evento E ⊆ U
La probabilità di un evento si misura con il rapporto p(E) = |E|/|U|
La probabilità, detta anche speranza matematica, misura il grado di (in)certezza sul verificarsi dell'evento, in un processo che progressivamente riduce l'insieme dei casi possibili, modificando le probabilità degli eventi
Ai connettivi proposizionali che possono formare congetture corrispondono le operazioni insiemistiche sugli eventi; in particolare, alla negazione della proprietà di E, che esclude il verificarsi di E, corrisponde l'evento complementare E = U\E, con p(E) = 1-p(E)
℘(U) è lo spazio degli eventi nello spazio campionario U :
Alcune relazioni binarie su ℘(U) sono particolarmente significative:
Quanto può influire sulla probabilità di un evento E1 l'informazione dell'essersi verificato un altro evento E2?
La probabilità condizionata p(E1|E2) di E1 rispetto a E2, con p(E2)>0, è definita da
Definizione : E1 è indipendente da E2 se p(E1|E2) = p(E1)
Fatto : su eventi di probabilità non nulla, la relazione di indipendenza è simmetrica, ovvero p(E1|E2) = p(E1) ⇔ p(E2|E1) = p(E2)
Fatto : se E1 ed E2 sono eventi indipendenti, allora p(E1∩E2) = p(E1)·p(E2)
Fonti di esempi ed esercizi proposti in questa lezione:
Approfondimenti di combinatoria e calcolo delle probabilità nel Bridge:
Per osservazioni, domande, proposte di soluzioni di esercizi ecc.: scrivere a
Buon divertimento!