principali criteri di qualità degli algoritmi

• correttezza: conditio sine qua non
• semplicità: utile a dimostrare la correttezza
• efficienza: utile in pratica per la scalabilità

il primo esercizio della lezione precedente suggerisce un promettente metodo di sviluppo di algoritmi per la soluzione di problemi di una certa complessità:

• partendo dalla descrizione del problema, ideare una soluzione ad alto livello di astrazione, in cui cioè si assuma che l'esecutore possa eseguire come primitive operazioni complesse, preoccupandosi solo che siano ben definite (e utili ;)
• procedere poi al raffinamento dell'algoritmo, affrontando il problema della realizzazione delle operazioni che, considerate primitive in prima approssimazione, risultano non esserlo per le effettive capacità dell'agente di calcolo

a ben vedere, la realizzazione di ciascuna delle operazioni da considerare nella fase del raffinamento costituisce a sua volta un problema al quale si cerca un soluzione algoritmica... si può dunque reiterare il metodo a ciascuno dei problemi della seconda fase, abbassando gradualmente il livello di astrazione in successivi passi di raffinamento, finché non rimane alcuna operazione che non sia effettivamente eseguibile

• legge di Pareto:
  • nei sistemi con un numero molto grande di parti
    più dell'80% dei fenomeni si deve a meno del 20% di esse
  • in grandi sistemi software, l'efficienza di alcuni algoritmi (<20%)
    è di cruciale importanza per le prestazioni del sistema
• efficienza di algoritmi  ≠ efficienza di codifica
  • ... la prima è molto più redditizia!
• efficienza e semplicità spesso in conflitto... (che fare?)
  • combinazione ottimale: algoritmo efficiente, codifica semplice
• valutazione delle prestazioni di un algoritmo:
  • analitica: può essere difficile, ma è rigorosa
  • empirica: sopperisce alle difficoltà di analisi

• formulazione matematica concisa: problema di
  • decisione di una relazione di equivalenza finita
• cioè, più precisamente:
  • date una relazione binaria simmetrica R, specificata da un insieme finito di coppie, e una coppia in input,
  • decidere se la coppia appartiene a R^*, la chiusura riflessiva e transitiva di R, ossia se, nel grafo non orientato che rappresenta R, esiste un cammino che connette gli elementi della coppia data
• il problema ha molte applicazioni pratiche, ad es.:
  • costruzione di reti (di calcolatori, elettriche, etc.)
  • problemi di unificazione
    (nella deduzione automatica, implementazione di linguaggi dichiarativi, etc.)

• più "semplice" (secondo (Sedgewick, 2002)):
  date M connessioni su N oggetti, dire se tutte le coppie di oggetti sono connesse
• N.B. è più "semplice" l'output, ma si richiede pur sempre un algoritmo per il problema di decisione enunciato sopra!
  • idea per la soluzione: output = albero di copertura?
  • tutte le coppie degli N oggetti sono connesse sse l'output dell'algoritmo per la precedente prima variante del problema di connettività consta di N-1 coppie

• idea essenziale: rappresentare le componenti connesse del grafo,
  cioè le classi di equivalenza di R^*
  • ogni nodo p del grafo appartiene a una e una sola componente connessa: C_p
  • operazione find: determina C_p, dato p
  • connettere due nodi fra i quali non c'è cammino nel grafo ne "fonde" le rispettive componenti connesse:
  • operazione union: unisce le componenti connesse C_p, C_q
• operazioni astratte facilmente riusabili per molti altri problemi
• soluzione astratta alla prima variante del problema:
  • per ogni coppia p-q in input:
  • C_p ← find(p), C_q ← find(q),
  • se C_p ≠ C_q  allora  union(C_p, C_q), output p-q

un algoritmo semplice (non troppo: non richiede memorizzazione di tutte le coppie in input)

si abbiano N nodi:   quale struttura dati concettuale di supporto all'algoritmo, introduciamo una sequenza di variabili id_i (i=1,...,N) che soddisfi l'invariante:

se c_n = p-q è la n-sima coppia in input, allora id_p = id_q sse C_p = C_q nel grafo costruito dalle coppie precedenti {c_m | m<n}

• inizializzazione: id_i ← i, 1 ≤ i ≤ N
• implementazione di union(C_p,C_q) :
  t ← id_p ; per 1 ≤ i ≤ N: se id_i = t allora id_i ← id_q
• implementazione di find(p) : immediata, grazie all'invariante
• efficienza dell'algoritmo quick-find : non entusiasmante ...
  esegue almeno MN istruzioni, per M operazioni di union

cosa è esattamente una sequenza?

• non un "insieme totalmente ordinato", perché ogni elemento di un insieme vi occorre una sola volta, mentre in una sequenza se ne possono avere più occorrenze

una sequenza è una funzione, definita su un dominio (totalmente ordinato) di indici

le sequenze sono strutture dati frequenti negli algoritmi; lo sono anche gli alberi:

• esempi: organigrammi, sistemi di file, strutture di libri, alberi sintattici, termini,...
• naturalmente associati allo sviluppo di algoritmi per raffinamenti successivi

cosa è esattamente un albero?

• albero libero: grafo (non orientato) connesso privo di cicli
  • equivalentemente: grafo in cui esiste un unico cammino fra ogni coppia di vertici
• albero (radicato): albero con un vertice designato, detto radice

sebbene il grafo di un albero sia generalmente non orientato, la designazione di un vertice radice induce naturalmente un ordinamento parziale dei vertici, grazie all'assenza di cicli, dunque un orientamento degli archi

• m<n se m precede n nel cammino dalla radice a n

terminologia: padre, figli, foglie, sottoalbero, ...

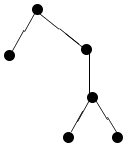
• alberi nella sequenza id nell'esecuzione di quick-find: ne sono radici i punti fissi della funzione id, cioè gli n tali che id_n = n

input: 3-4, 4-1, 5-2, 0-2

• possiamo modificarli per una più efficiente esecuzione di union
• nuovo invariante: ( id^ωp : radice dell'albero a cui appartiene p )

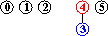
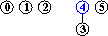
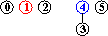
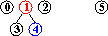
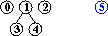
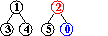
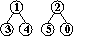
C_p = C_q nel grafo costruito dalle coppie precedenti p-q sse id^ωp = id^ωq

• inizializzazione: come in quick-find
• implementazione di find(p)
• si complica: i ← id^ωp
• implementazione di union(C_p,C_q)
• immediata: id_i ← id_j

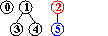
input: 3-4, 4-1, 5-2, 3-5

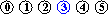
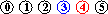
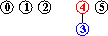
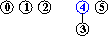
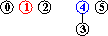
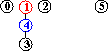
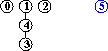
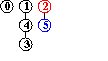
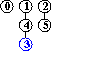
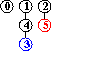
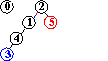
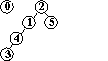
efficienza dell'algoritmo quick-union : non sempre buona, può dover eseguire più di MN/2 istruzioni (per N nodi e M coppie in input), se M>N

• quick-union : cammini lunghi da foglia a radice, anche fino a N-1 passi
  • (!) possiamo intervenire su questo per ottenere una find più rapida
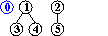
• l'invariante di quick-union permane, ma fra due nodi id^ωp ≠ id^ωq da connettere per union, manteniamo la radice dell'albero più grande
• per tener traccia della dimensione dell'albero che nella sequenza id sottende ciascun nodo, usiamo una sequenza ausiliaria sz_i , i = 1,...,N

• inizializzazione: come in quick-union, ma estesa alla sequenza ausiliaria sz
• implementazione di find(p) : invariata
• implementazione di union(C_p,C_q) : si complica un po' per tener conto di, e aggiornare, sz

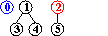
input: 3-4, 4-1, 5-2, 3-5

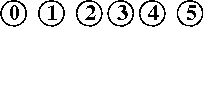
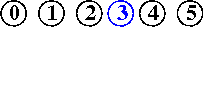
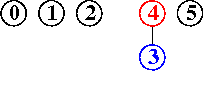
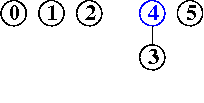
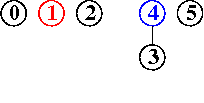
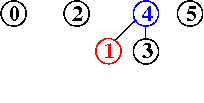
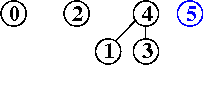
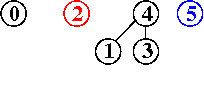
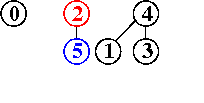
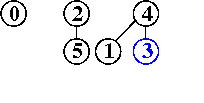
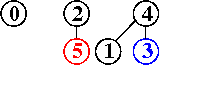
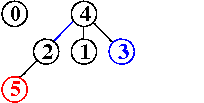
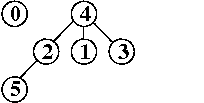
efficienza di quick-union pesata : molto migliore della precedente, per la riduzione della lunghezza dei cammini, proporzionale non più a N bensì a lg N, anche nel caso peggiore

che "lezione di metodo" trarre dallo studio condotto sul problema della connettività?

punti salienti dello schema di studio degli algoritmi union-find:

• specifica chiara ed esatta dell'enunciato del problema
• analisi dell'enunciato
  • per l'identificazione delle operazioni astratte intrinseche del problema
• sviluppo di un primo algoritmo
  • semplice, di immediata correttezza in termini delle operazioni astratte
• implementazione semplice in un primo programma
  • con una codifica delle operazioni astratte su strutture dati atte allo scopo
• miglioramento dell'efficienza per raffinamenti successivi
  • valutandone l'efficacia con analisi formali e/o valutazioni empiriche
• uso di rappresentazioni astratte di strutture dati e algoritmi impiegati
  • per la progettazione ad alto livello delle successive versioni
• analisi prestazionale (caso peggiore e medio) per trarne garanzie di efficienza