Docente:
Giuseppe Scollo
Università di Catania
Facoltà di Scienze Matematiche, Fisiche e Naturali
Corso di Laurea in Informatica, I livello, AA 2009-10
precursori della formalizzazione logica: da Aristotele a Leibniz
Leibniz anticipa di un paio di secoli l'intuizione di George Boole: le leggi di un'algebra del pensiero
in prima approssimazione: un insieme + operazioni su di esso
le equazioni giocano un ruolo fondamentale nell'algebra tradizionale:
le equazioni sono non meno fondamentali nell'algebra astratta (XX secolo):
cos'è un'operazione?
questa definizione corrisponde al concetto intensionale di funzione, dove è rilevante il modo in cui si determina l'immagine di ciascun elemento del dominio di definizione
un'operazione di arietà k, o k-aria, ha argomenti nel prodotto cartesiano di k insiemi
una proprietà è un'operazione che produce risultati in un insieme di due valori, usualmente detti valori di verità ({0,1}, o {T,F}, etc.)
la versione estensionale del concetto di proprietà corrisponde al concetto insiemistico di relazione k-aria: sottoinsieme del prodotto cartesiano di k insiemi
quasi-ordine (o preordine):
una relazione binaria ≼
su un insieme la quale soddisfi:
≼ x
≼
y , y ≼ z →
x ≼ z
N.B. la relazione conversa di un quasi-ordine è anch'essa un quasi-ordine
relazione di equivalenza:
un quasi-ordine ≈
su un insieme che inoltre soddisfi:
≈ y →
y ≈ x
N.B.: la congiunzione (o, insiemisticamente, intersezione) di un quasi-ordine e della sua conversa è una relazione di equivalenza: il kernel del quasi-ordine
una relazione binaria su un insieme è un ordinamento stretto se è irriflessiva (cioè non vale mai per una coppia di elementi identici) e transitiva
ordinamento parziale: un quasi-ordine ≤
su un insieme che inoltre soddisfi:
≤
y , y ≤ x →
x = y
terminologia: se ≤
è un ordinamento parziale:
≤
b, allora a
è un
minorante di b,
e b è un
maggiorante di a
il concetto di algebra, nella prima approssimazione introdotta sopra, si generalizza a quello di struttura algebrica, in cui si distingue:
una ridotta di una struttura A è una struttura costituita da un sottoinsieme delle operazioni e relazioni di A, definite sullo stesso sostegno
una struttura si dice omogenea se il sostegno consta di un solo insieme, eterogenea altrimenti (N.B.: il sostegno di una ridotta di una struttura eterogenea A può essere costituito da un sottoinsieme proprio della collezione di insiemi che costituisce il sostegno di A, purché tutte le operazioni della ridotta siano definite nel suo sostegno)
una struttura dotata solo di operazioni totali è detta algebra in senso stretto, altrimenti è un'algebra in senso lato
N.B.: è sempre possibile rappresentare una struttura algebrica come
semigruppo:
(A; ⋅ ),
con ⋅
un'operazione binaria associativa
monoide:
(A; e, ⋅ ),
un semigruppo
(A; ⋅ )
con e costante
neutra rispetto a
⋅
gruppo [commutativo]:
(A; e, ⋅, — ),
un monoide [commutativo] (A; e, ⋅ )
con un'operazione unaria
—
che dà l'inverso rispetto a
⋅
ed e: x⋅—x
= —x⋅x
= e
semianello [commutativo]:
(A; 0, 1, +, ⋅),
un monoide commutativo (A; 0, +), detto additivo, e
un monoide [commutativo] (A; 1, ⋅), detto
moltiplicativo, tali da soddisfare:
⋅(y+z)
=
(x⋅y)
+
(x⋅z),
(x+y)⋅z
=
(x⋅z)
+
(y⋅z)
⋅ x
=
x ⋅ 0
= 0
anello [commutativo]:
(A; 0, 1, +, ⋅, —),
un semianello [commutativo]
(A; 0, 1, +, ⋅), con il monoide
additivo esteso a un gruppo commutativo (A; 0, +, —)
classi di algebre in senso stretto quali quelle viste in precedenza sono caratterizzate da assiomi di forma molto semplice:
= t2
quando una classe di algebre è caratterizzata da un insieme di equazioni, che ne costituisce la base assiomatica, è possibile dedurre da tale base tutte le equazioni valide in ogni algebra della classe mediante le regole del calcolo equazionale di Garrett Birkhoff:
= t
= t2
allora
t2
= t1
= t2,
t2
= t3
allora
t1
= t3
= t2
allora
τ(t1)
=
τ(t2)
= t2
allora
t[u←t1]
=
t[u←t2]
dove il termine
τ(t) è ottenuto dal termine
t per sostituzione simultanea di tutte
le occorrenze di ciascuna variabile con uno stesso termine, mentre il termine
t[u←t']
è ottenuto dal termine
t rimpiazzando il suo sottotermine
al posto u
con il termine t'
def.: un reticolo è un ordinamento parziale in cui ogni coppia di elementi abbia:
alternativamente, per via strettamente algebrica:
⋅
è espressa dall'equazione x⋅x = x)
∨,∧)
tale che le sue due
algebre ridotte
(A; ∨),
(A; ∧)
sono semireticoli, e inoltre valgono gli assiomi di assorbimento:
∨
(x ∧
y) = x
x ∧
(x ∨
y) = x
che fine ha fatto l'ordinamento del reticolo? può essere definito algebricamente come abbreviazione di equazioni nelle due operazioni binarie:
≤
y
≡
x
∨
y
=
y
oppure:
x
≤
y
≡
x
∧
y
=
x
N.B.: si veda in proposito l'esercizio sull'ordinamento nei reticoli algebrici
un reticolo è completo se ogni insieme di suoi elementi ha un minimo maggiorante e un massimo minorante
un reticolo è detto distributivo se ciascuna delle sue due operazioni è distributiva rispetto all'altra
caratterizzazione M3-N5 dei reticoli non distributivi:
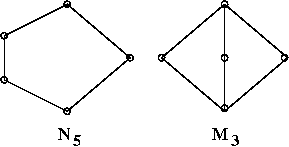
un reticolo è detto limitato se ha un massimo 1 e un minimo 0
un reticolo limitato è detto complementato
se ammette un'operazione unaria di complemento
- tale da soddisfare:
x
∨
-x
= 1
e:
x
∧
-x
= 0
un'algebra di Boole è un reticolo distributivo complementato
mettendo assieme le equazioni che caratterizzano i reticoli distributivi complementati, si ottiene una base assiomatica di 12 equazioni per le algebre di Boole
un paio di domande si sono presto imposte all'attenzione:
alla risposta (negativa) alla prima domanda ha fatto seguito la ricerca di di una risposta alla seconda, con riferimento alla ridotta costituita da una delle due operazioni di reticolo e dal complemento
una celebre assiomatizzazione delle algebre di Boole (A; +, —) così
ridotte, dovuta a E.V. Huntington (1933),
consta di solo 3 equazioni:
associatività e commutatività di + e:
—(—x + y)
+ —(—x +
—y)
= x
è l'assiomatizzazione più economica? v. il tema di approfondimento 2