un sistema di transizioni di stato è una struttura relazionale dotata di una costante e di una relazione binaria

• il sostegno è l'insieme degli stati del sistema, la costante ne è lo stato iniziale, la relazione binaria è detta relazione di transizione

è spesso utile in pratica distinguere fra diversi tipi di transizioni di stato,

• ad es. in sistemi dove le transizioni sono attivate da input diversi

un sistema di transizioni etichettate (ingl. labelled transition system (LTS)) generalizza il concetto ammettendo una famiglia di relazioni di transizioni, dove i simboli delle relazioni costituiscono l'insieme delle etichette del sistema

• ciò si rappresenta graficamente etichettando con i rispettivi simboli gli archi di transizione nel diagramma del sistema

un LTS è deterministico se le sue relazioni di transizione sono funzioni, altrimenti è non deterministico

• in un sistema deterministico, dove le etichette rappresentino i diversi valori dell'input, in qualsiasi stato per ogni valore dell'input esiste al più uno stato al quale il sistema possa transire da quello stato e per quell'input

quando l'insieme degli stati è finito, il sistema è detto a stati finiti

una macchina a stati finiti (ingl. finite state machine (FSM)) è un LTS a stati finiti con un insieme finito di etichette, che ne designano le interazioni con l'ambiente

è spesso utile, ad es. per la modellazione di circuiti sequenziali, distinguere le interazioni di input da quelle di output di una FSM

• in una macchina di Moore l'output prodotto dipende solo dallo stato di arrivo di una transizione, ed è ad esso associato
• in un macchina di Mealy l'output dipende dallo stato e dall'input, ed è perciò associato alle transizioni

la distinzione fra input e output nelle interazioni permette l'interconnessione di FSM, ed eventualmente la sincronizzazione delle rispettive transizioni di stato determinate da una interazione di I/O tra FSM interconnesse

• spesso si estende il modello di interconnessione con l'ipotesi di interazioni asincrone, assumendo l'esistenza di code FIFO quali canali di comunicazione

quando le code sono di capacità limitata, il modello asincrono può essere ridotto a quello sincrono rappresentando le code stesse come FSM

• altrimenti è rappresentabile come un LTS

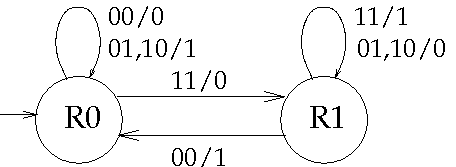
il comportamento di un circuito sommatore può essere facilmente modellato da una FSM con output

• vogliamo che la macchina riceva in input una sequenza di coppie di bit (di uguale significatività, nella rappresentazione binaria degli addendi), e produca in output la rappresentazione binaria naturale della loro somma

possiamo tener conto del riporto da ciascuna posizione alla successiva dotando la macchina di due stati, corrispondenti ai due valori del riporto

• in tal modo l'output prodotto dipende sia dallo stato che dall'input, perciò usiamo una macchina di Mealy, con stato iniziale quello di riporto nullo:

come accennato nella lezione precedente, l'impiego di una macchina a stati finiti quale riconoscitore di un linguaggio non richiede interazioni di output, bensì la qualifica di un sottoinsieme F degli stati quali stati finali o accettanti

• un automa a stati finiti (FSA) accetta una stringa w∈Σ* se ha una sequenza di transizioni, dallo stato iniziale ad uno stato finale, con sequenza di etichette w
• il linguaggio riconosciuto da un FSA è l'insieme delle stringhe che esso accetta

formalmente, un FSA è una quintupla <Q, Σ,, δ, q₀, F>, dove Σ è l'alfabeto di input e gli altri simboli hanno il significato già detto

• quando la dinamica δ è una funzione δ : Q X Σ → Q, l'automa è deterministico (DFA), altrimenti è non deterministico (NFA), nel qual caso si può trattare la dinamica come una funzione avente per codominio l'insieme delle parti di Q, δ : Q X Σ → ℘(Q)

è conveniente pensare a un NFA come in grado di transire simultaneamente a tutti gli stati permessi dalla dinamica, per un dato input e in un dato insieme di stati in cui si trovi

un FSA è un riconoscitore privo di memoria, dunque il solo modo di tener traccia di eventi accaduti, significativi per il riconoscimento, sta nel definire stati distinti a tal fine

• ad es., un DFA che riconosce (soltanto) la parola then sull'alfabeto inglese avrà 5 stati ed un'unica sequenza accettante

il fatto che uno stato sia finale non implica assenza di transizioni uscenti da esso

• si tracci ad es. il diagramma di transizione di un DFA che riconosca il linguaggio delle sequenze binarie prive di bit consecutivi uguali: {ε,0,1,01,10,010,101,...}

per definire con precisione il linguaggio accettato da un DFA, estendiamo la sua funzione di transizione sì da considerare stringhe sul suo alfabeto quale input:

• sia δ* : Q X Σ* → Q tale funzione di transizione estesa, definita per induzione sulla lunghezza della stringa argomento: δ*(q,ε) = q, δ*(q,wa) = δ(δ*(q,w),a)

con la notazione introdotta, il linguaggio L_A riconosciuto dall'automa A è definito da L_A = {w | δ*(q₀,w) ∈ F }

la sola differenza di definizione formale tra DFA e NFA sta nel tipo della funzione di transizione, che per un NFA assegna a uno stato q e ad un'etichetta a l'insieme δ(q, a) degli stati ai quali l'automa può transire con l'input a

• ciò richiede una diversa definizione formale della funzione di transizione estesa a stringhe in input, ancora per induzione sulla lunghezza della stringa argomento: δ*(q,ε) = {q}, δ*(q,wa) = ∪_{p∈δ^*(q,w)}δ(p,a)

coerentemente con tale modifica, e con la condizione di accettazione di stringhe da un NFA, il linguaggio L_A riconosciuto dall'automa non deterministico A è definito da L_A = {w | δ*(q₀,w) ∩ F ≠ ∅ }

• ecco ad es. un NFA che riconosce il linguaggio { x01 | x ∈ {0,1}^* } :

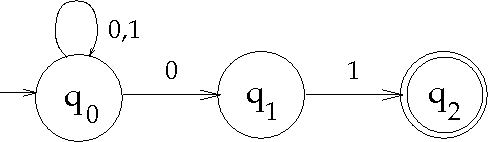
una costruzione canonica di un DFA che riconosce lo stesso linguaggio di un dato NFA è fatta così (il pedice D o N, nella designazione di componenti di un automa, rispettivamente indica l'automa da costruire o quello dato):

• Q_D = ℘(Q_N),  q_0D = {q_0N },  δ_D(q_D, a) = ∪_q∈qDδ_N(q, a),  F_D = {q_D | q_D ∩F_N ≠ ∅ }

in pratica, spesso molti degli insiemi in ℘(Q_N) sono stati non raggiungibili dallo stato iniziale nel suo DFA equivalente canonico, e possono pertanto essere eliminati

• ad es., la costruzione canonica del DFA equivalente al NFA della pagina precedente ne genera uno con 8 stati, ma di questi solo 3 sono raggiungibili dallo stato iniziale {q₀}:  {q₀},  {q₀, q₁},  {q₀, q₂}

N.B. l'insieme vuoto di stati del NFA è uno stato del DFA equivalente canonico, ed è raggiungibile dallo stato iniziale sse per qualche stringa di input nessuno stato è raggiungibile dallo stato iniziale nel NFA con quell'input

• nell'esempio precedente si ottiene un DFA equivalente al NFA dato con lo stesso numero di stati; possiamo sempre trovare un DFA equivalente di dimensione prossima a quella del NFA dato?

nel caso peggiore, il minimo numero di stati necessari a costruire un DFA equivalente a un NFA dato è esponenzialmente maggiore del numero di stati del NFA, come accade nel seguente caso

• è dato un NFA che riconosce tutte e soltanto le stringhe binarie il cui n-simo bit prima della fine è 1:

• teorema: nessun DFA equivalente a questo NFA può avere meno di 2ⁿ stati

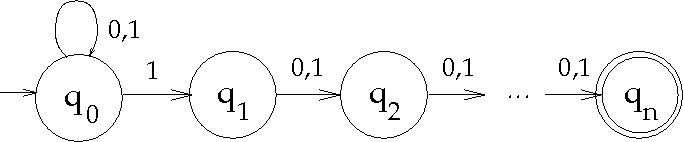
per fortuna, il caso peggiore non sempre si verifica...

• esistono, anzi, casi di notevole interesse pratico in cui è agevole la costruzione di un DFA equivalente con un numero di stati non superiore a quello del NFA: vediamone uno...

un problema frequente nella pratica è la ricerca di una qualsiasi stringa da un dato insieme, diciamo delle parole indicizzate, in un testo

• un automa che decide l'esistenza o meno di una tale stringa nel testo è quello che accetta il linguaggio delle stringhe con un suffisso nell'insieme indicizzato

un approccio alternativo, frequente in alcune applicazioni, richiede la costruzione di un indice invertito delle occorrenze delle stringhe ricercabili nel testo

• questo è oneroso quando l'insieme delle parole indicizzate muta spesso, o non può essere costruito: in tal caso la costruzione dell'automa risulta più conveniente

un NFA che accetta il linguaggio suddetto è quello che ha la seguente "struttura a pettine":

• per ogni simbolo dell'alfabeto, una transizione dallo stato iniziale in se stesso
• per ogni parola indicizzata, sia k la sua lunghezza, una sequenza di k stati ai quali l'automa transisce a partire dallo stato iniziale, con transizioni progressivamente etichettate dai simboli della parola, e terminante in uno stato finale

teorema: esiste un DFA equivalente al NFA dato con un numero non superiore di stati

una estensione degli NFA, che non ne estende la classe dei linguaggi da essi riconoscibili, permette transizioni prive di etichetta dall'alfabeto di input

• tali ε-transizioni sono spesso, per convenienza, "etichettate" con il simbolo della stringa vuota, ma si richiede che ε non sia un simbolo dell'alfabeto di input

come vedremo presto, una delle ragioni di interesse a questa estensione degli NFA sta nel fatto che rende agevole la dimostrazione di equivalenza di FSA ed espressioni regolari

un ε-NFA è definito come un NFA, ma con una funzione di transizione su Q X (Σ∪{ε})

• si definisce quindi la ε-chiusura q^(ε) di uno stato q dell'ε-NFA come l'insieme di stati raggiungibili da q con una sequenza (anche vuota) di transizioni di etichetta ε;
• la ε-chiusura di un insieme di stati S è definita come l'unione delle ε-chiusure degli stati in S

la funzione di transizione estesa alle stringhe in input è così definita per un ε-NFA:

• δ*(q,ε) = q^(ε) ,  δ*(q,wa) = (∪_{p∈δ^*(q,w)}δ(p,a))^(ε)

il linguaggio riconosciuto da un ε-NFA è definito come per un NFA, ma con questa δ*

la costruzione canonica del DFA equivalente a un ε-NFA è analoga a quella per un NFA, ma con la differenza che gli stati raggiungibili dallo stato iniziale di questo DFA sono ε-chiusi

• formalmente, il DFA D equivalente all'ε-NFA N ha:
  Q_D = ℘(Q_N),  q_0D = q_0N^(ε) ,  δ_D(q_D, a) = (∪_q∈qDδ_N(q, a))^(ε),  F_D = {q_D | q_D ∩F_N ≠ ∅ }

teorema: un linguaggio è accettato da un ε-NFA se e solo se è accettato da un DFA

• solo se: per induzione sulla lunghezza delle stringhe accettate, usando la costruzione canonica del DFA equivalente
• se: si trasforma il DFA in un ε-NFA rimpiazzando ogni stato con il singoletto che lo contiene, ed estendendo la funzione di transizione con una ε-transizione da ciascun singoletto all'insieme vuoto

1. Equivalenze di automi
   l'equivalenza di automi quali riconoscitori di linguaggi è appropriata alla teoria dei linguaggi formali, mentre non lo è per altre teorie, in cui gli automi sono modelli matematici di processi interagenti e comunicanti. In queste teorie, ad es. il Calculus of Communicating Systems (CCS) di Milner, o i Communicating Sequential Processes (CSP) di Hoare, generalmente si adottano equivalenze più restrittive, che richiedono l'indistinguibilità del comportamento osservabile di automi equivalenti. Diverse equivalenze sono state studiate in tal senso, da quelle di bisimulazione ad altre equivalenze, dette di testing, meno restrittive delle bisimulazioni (che in un certo senso "discriminano troppo"), ma più di quella della teoria dei linguaggi formali. Una ricognizione sulle diverse semantiche degli automi esula dai limiti dell'insegnamento, ma è un tema meritevole di approfondimento.