• a che serve l'analisi delle prestazioni degli algoritmi:
  • confrontare algoritmi diversi per uno stesso problema
  • stimare le prestazioni di algoritmi indipendentemente dal linguaggio di programmazione e dall'ambiente operativo
  • ottimizzare eventuali parametri degli algoritmi
• cosa serve per l'analisi delle prestazioni degli algoritmi:
  • alcuni (pochi) concetti matematici fondamentali (v. appresso)
  • analisi disponibili in letteratura per algoritmi di ampia applicabilità
• problemi inerenti dell'analisi degli algoritmi:
  • stima approssimata (quella esatta può essere difficile)
  • algoritmi diversi possono avere prestazioni incomparabili (ad es. con ampie e diverse fluttuazioni al variare dell'input)
• quali analisi sono rilevanti:
  • caso medio: si assume che l'input sia generato casualmente
  • caso peggiore: si determina l'input appropriato da analisi di algoritmo e dati

consideriamo l'algoritmo di ricerca di un nome in un elenco proposto in una lezione precedente

• per vedere come il tempo impiegato dall'algoritmo dipenda dalla dimensione dell'input (numero di elementi nell'elenco), basta considerare solo il ciclo

riguardo alla dipendenza dal valore dell'input, dobbiamo considerare due casi

• o il nome è nell'elenco: esito positivo
• o si esaurisce lo spazio di ricerca: esito negativo

se l'elenco ha N nomi, la ricerca sequenziale esamina mediamente :

• N elementi in caso di esito negativo
• all'incirca N/2 elementi in caso di esito positivo
  • esattamente:   (N+1)/2

la ricerca sequenziale esamina N elementi nel caso peggiore, in qualsiasi esito

assunto: dipendenza delle prestazioni dell'algoritmo da un parametro primario N

(uno solo, per semplicità e senza perdita di generalità)

il tempo di esecuzione ("costo" più significativo degli algoritmi nella maggior parte dei casi) tipicamente cresce come una delle seguenti funzioni di N, e la rispettiva crescita si dice:

• 1 : costante (crescita zero)
• log N : logaritmica
• N : lineare
• N log N : poco più che lineare ("linearitmica"?)
• N² : quadratica
• N³ : cubica
• 2^N : esponenziale

nell'esempio precedente, non c'è alternativa alla ricerca sequenziale se l'elenco non è ordinato

se l'elenco dei nomi è ordinato (in un qualsiasi ordinamento totale), la prestazione media della ricerca sequenziale può migliorare nel caso di esito negativo, arrestando l'esecuzione del ciclo quando l'elemento confrontato con il nome dato è maggiore di questo (se l'ordine è ascendente)

• la prestazione media eguaglia in tal caso quella dell'esito positivo
• il costo computazionale della ricerca sequenziale è comunque lineare

se l'elenco è ordinato, si può fare (molto) meglio!

l'idea dell'algoritmo di ricerca binaria è la seguente:

• si esegue il primo confronto con l'elemento in posizione centrale (o quasi, se N è pari) nell'elenco
• se il confronto ha esito negativo, si riapplica lo stesso procedimento
  • al semielenco superiore, se l'elemento centrale è minore del nome dato
  • al semielenco inferiore altrimenti

la ricerca binaria, ad ogni passo con esito negativo dimezza la dimensione dello spazio di ricerca nel passo successivo

• ne consegue che il costo computazionale della ricerca binaria è proporzionale a lg N (anche nel caso peggiore)

il guadagno di efficienza rispetto alla ricerca sequenziale è esponenziale!

come nel caso dell'algoritmo di quick-union pesata, il guadagno di efficienza è dovuto all'operare lungo un cammino, in questo caso da radice a foglia, di un albero bilanciato, di altezza logaritmica rispetto al numero dei nodi

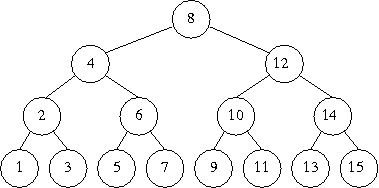
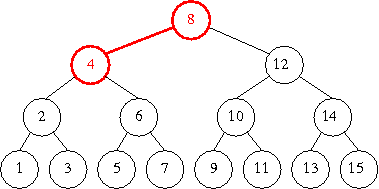
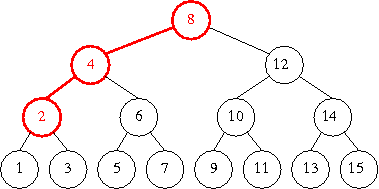
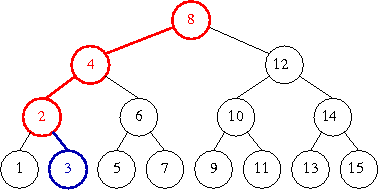
a mo' di esempio, l'albero in figura rappresenta le opzioni disponibili alla ricerca binaria di un numero nell'elenco ordinato dei numeri da 1 a 15, ed il cammino in rilievo mostra le scelte fatte per la ricerca di 3

albero di ricerca binaria dei numeri da 1 a 15

definizione: funzione inversa dell'esponenziale

ovvero, log_b x è l'esponente da dare a b per ottenere x :

• b^{log_b x} = x
• log_b b^x = x

dalla definizione discendono le proprietà:

• reciprocità :   log_b a = 1 / log_a b
• additività :     log_b xy = log_b x + log_b y ,     log_b (x /y) = log_b x - log_b y

notazione per basi speciali:

• logaritmo naturale :   ln x = log_e x
• logaritmo binario :     lg x = log₂ x

un'applicazione delle approssimazioni intere del logaritmo binario:

• per la codifica binaria di N+1 oggetti distinti occorrono ⌊lg N⌋+1 = ⌈lg(N+1)⌉ bit

le prestazioni della ricerca binaria si devono all'ipotesi che lo spazio di ricerca sia ordinato

• qual è il costo computazionale di un algoritmo di ordinamento? dipende dall'algoritmo ;)

un metodo semplice può usare come primitiva una vecchia conoscenza: una funzione di ricerca del massimo in un insieme, per la quale già disponiamo di un algoritmo

nel nostro caso occorre però un algoritmo un po' diverso, perché vogliamo ordinare una sequenza data, non necessariamente di numeri, e ci serve una funzione che ci dia la posizione (ad es., della prima occorrenza) del massimo elemento trovato nella sequenza

tali adattamenti sono proposti come esercizi, assieme ad altri raffinamenti del seguente algoritmo di ordinamento, in cui A = A₁ ... A_N è la sequenza data, e dove indichiamo con il termine procedura un algoritmo che può modificare i dati che riceve in ingresso

• procedura   ordina (A)
• finale ← lunghezza(A)
• finché finale > 1 ripeti:
•     m ← posizioneMassimo(A, finale)
•     scambia(A, m, finale)
•     finale ← finale - 1
• fine ciclo

possiamo ora rispondere alla domanda posta all'inizio della pagina precedente, con riferimento all'algoritmo appena visto, ragionando come segue:

• basta considerare il costo computazionale del ciclo
• il ciclo, valutazione della condizione inclusa, viene eseguito N volte
• in ciascuna iterazione, tutte le operazioni eseguite hanno costo costante (indipendente da N), tranne la funzione posizioneMassimo, che determina la posizione del massimo nella parte non ancora ordinata della sequenza
• posizioneMassimo alla k-sima iterazione esegue N-k confronti, dunque il suo costo totale è quadratico, mentre il costo totale delle altre operazioni del ciclo è lineare
• ne consegue che il costo computazionale dell'algoritmo è quadratico

sorgono spontanee due domande:

1. il costo dell'ordinamento non vanifica il guadagno di efficienza della ricerca binaria?
2. non esistono algoritmi di ordinamento (decisamente) più efficienti?

rispondiamo nell'ordine:

1. no, se la ricerca va eseguita molte volte sulla sequenza data: l'ordinamento è un "investimento", il cui costo si ammortizza sulle numerose esecuzioni della ricerca
2. sì, sono noti algoritmi di ordinamento di costo proporzionale a   N lg N

la limitazione asintotica espressa dalla notazione O grande non è sufficiente a caratterizzare la velocità di crescita

• ad esempio: kN è O(N²) ma ha crescita lineare, non quadratica

la notazione  ≈  (letta "all'incirca") designa l'approssimazione asintotica di una funzione con un'altra:

def. :   f(N) ≈ g(N) se  f(N) = g(N)+h(N)  e  h(N)/g(N) → 0 per N → ∞

per caratterizzare solo la velocità di crescita l'approssimazione asintotica chiede troppo... basta invece il seguente concetto

la notazione  ∝  (letta "proporzionale a") designa la proporzionalità asintotica di una funzione ad un'altra:

def. :   f(N) ∝ g(N) se esiste una costante c tale che   f(N) ≈ cg(N)

finora si sono considerate stime e analisi delle prestazioni di algoritmi per un dato problema, o classe di problemi, e per essi risulta utile distinguere fra

• caso peggiore : l'analisi delle prestazioni in tal caso fornisce garanzie sul costo computazionale dell'algoritmo
• caso medio : l'analisi delle prestazioni in tal caso fornisce una stima del costo computazionale mediamente atteso

per complessità computazionale di un problema si intende:

• il costo computazionale nel caso peggiore del miglior algoritmo per quel problema

il costo computazionale nel caso peggiore di un algoritmo per un dato problema costituisce un limite superiore alla complessità computazionale del problema:

• il costo del miglior algoritmo non può superare quello di qualsiasi algoritmo

è anche utile determinare limiti inferiori alla complessità computazionale di problemi, analizzandone caratteristiche inerenti, ma questo compito è di solito più difficile