un'algebra di Kleene è un semianello dotato di una ulteriore operazione unaria, la chiusura di Kleene, che gode le seguenti proprietà:

• l'operazione additiva del semianello è idempotente:   x + x = x
  • ciò induce un ordinamento parziale sul sostegno mediante la definizione: x ≤ y ⇔ x + y = y
• l'operazione unaria, designata da un operatore postfisso "^*" (che ha precedenza su "⋅", che ha precedenza su "+"), soddisfa i seguenti assiomi (Kozen, 1990):
  • 1 + x⋅x^* ≤ x^*
  • 1 + x^*⋅x ≤ x^*
  • x⋅y ≤ y → x^*⋅y ≤ y
  • x⋅y ≤ x → x⋅y^* ≤ x

da questi assiomi discende, fra altre, la proprietà di chiusura dell'operazione unaria:

• x^**= x^*

la sintassi delle espressioni regolari è quella dei termini di un'algebra di Kleene, ma con alcune convenzioni notazionali:

• ε designa il neutro del monoide moltiplicativo ("1" negli assiomi precedenti)
• ∅ designa il neutro del monoide additivo
• l'operatore binario infisso "invisibile" designa l'operazione binaria moltiplicativa
• in luogo delle variabili si impiegano simboli (di costante) di un alfabeto prefissato

si ha così la notazione vista per l'algebra delle stringhe, estesa con gli operatori ∅, +, ^*, con le regole di precedenza già indicate, sovvertibili mediante l'uso di parentesi

la semantica di un'espressione regolare è data da un linguaggio sull'alfabeto costituito dai suoi simboli di costante (esclusi i simboli ∅, ε, che designano linguaggi e non sono elementi dell'alfabeto)

• un linguaggio è detto regolare se è specificabile da un'espressione regolare

per rendere esatta questa definizione dobbiamo definire l'interpretazione che i suddetti operatori hanno nell'algebra di Kleene dei linguaggi regolari

le operazioni sui linguaggi, su un alfabeto Σ, viste in una lezione precedente, offrono una naturale interpretazione agli operatori dell'algebra di Kleene

• l'algebra dei linguaggi regolari sull'alfabeto Σ, ha inoltre i singoletti dei simboli di Σ quali costanti, oltre all'insieme vuoto e all'insieme {ε } quali elementi neutri, risp., delle operazioni binarie di unione e di concatenazione di insiemi di stringhe

uno stesso linguaggio può essere specificato da diverse espressioni regolari, che sono pertanto equivalenti

esempio: il linguaggio delle stringhe binarie a bit alterni, cioè nelle quali i bit in posizioni consecutive sono sempre diversi, può essere descritto dalla seguente espressione regolare:

• (01)^*+ (10)^*+ 1(01)^*+ 0(10)^*

o, equivalentemente, dalla seguente espressione regolare:

• (1+ε)(01)^*(0+ε)

N.B. si noti la seguente equivalenza, deducibile dagli assiomi di algebra di Kleene: ∅ ^* = ε

espressioni regolari e automi a stati finiti definiscono la stessa classe di linguaggi, ovvero la classe dei linguaggi regolari, che coincide con la classe dei linguaggi di tipo 3 nella gerarchia di Chomsky

• nella lezione precedente è stata già vista l'equivalenza dei diversi tipi di FSA: DFA, NFA, ε-NFA

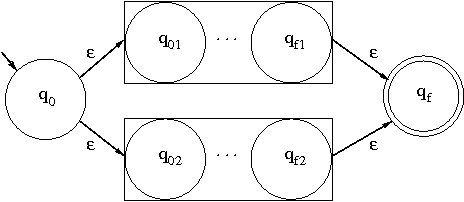
mostriamo allora l'equivalenza di espressioni regolari e FSA esibendo:

• per ogni DFA, una espressione regolare che definisce il linguaggio da esso accettato
• per ogni espressione regolare, un ε-NFA che accetta il linguaggio da essa definito

N.B. l'asimmetria in questa scelta obbedisce a un criterio di semplicità della dimostrazione

si ha una dimostrazione per induzione sul numero di stati, ma è alquanto intricata (seppur interessante proprio per questo)

• inoltre, la dimensione dell'espressione regolare ha crescita esponenziale

una alternativa più pratica è la costruzione dell'espressione regolare per progressiva eliminazione di stati del DFA

• si adopera a tal fine una nozione estesa di FSA, le cui transizioni sono etichettate da espressioni regolari

la struttura della costruzione è la seguente:

• per ogni stato accettante q, si eliminano progressivamente tutti gli stati, eccetto q stesso e lo stato iniziale q₀
• si ottiene così un FSA esteso a due stati, se q ≠q₀, a un solo stato altrimenti
• l'espressione regolare equivalente a ciascun FSA esteso così ottenuto è di immediata costruzione
• quella cercata è la somma delle espressioni regolari ottenute al variare di q in F

eliminazione di uno stato in un FSA esteso

• (figura)

estensione delle etichette di archi fra stati adiacenti: R'_ij = R_ij + P_i S^*Q_j

FSA esteso, ridotto a due stati

• (figura)

espressione regolare equivalente: (R + SU^*T)^*SU^*

FSA esteso, ridotto a uno stato

• (figura)

espressione regolare equivalente: R^*

la costruzione di un ε-NFA che accetta il linguaggio di una data espressione regolare E procede per induzione sulla struttura di E, rispettando un invariante che vale per qualsiasi ε-NFA così costruito:

• un solo stato finale, nessuna transizione allo stato iniziale, nessuna dallo stato finale

base dell'induzione: siffatti automi per le espressioni regolari ε, ∅, a, rispettivamente:

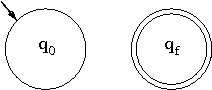
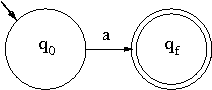
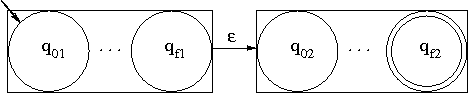
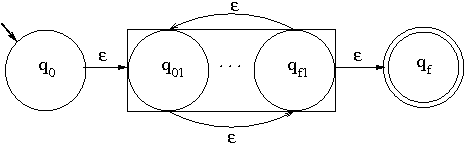
passo induttivo: composizione di siffatti automi per gli argomenti degli operatori +, _ _, ^*:

1. algebre di Kleene
   
2. applicazioni e varianti delle espressioni regolari